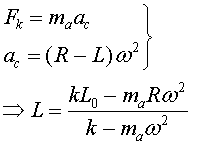Les forces d'inèrcia, existeixen?
Introducció
 La
veritat és que és molt difícil convèncer els estudiants
que el pessigolleig que senten quan pugen a les muntanyes russes és degut
a unes forces que no existeixen. El problema sorgeix molt cops perquè
el debat queda tallat amb aquesta negació existencial tan severa. El
que podem fer és trobar explicacions a aquestes sensacions sense necessitat
de carregar les tintes amb qüestions existencials. En tot cas l'existència
o no d'aquestes forces dependrà de si les necessitem o no per explicar
el que ens envolta. Com passa en altre casos, la força no és un
concepte absolut.
La
veritat és que és molt difícil convèncer els estudiants
que el pessigolleig que senten quan pugen a les muntanyes russes és degut
a unes forces que no existeixen. El problema sorgeix molt cops perquè
el debat queda tallat amb aquesta negació existencial tan severa. El
que podem fer és trobar explicacions a aquestes sensacions sense necessitat
de carregar les tintes amb qüestions existencials. En tot cas l'existència
o no d'aquestes forces dependrà de si les necessitem o no per explicar
el que ens envolta. Com passa en altre casos, la força no és un
concepte absolut.
Analitzem quan i com hem d'entendre els efectes de l'inèrcia.
No podem dir simplement "la força centrífuga no existeix"
i no atribuir a cap força les nostres "sensacions internes".
La llei de moviment de Newton
Una força sobre un objecte de massa m
l'accelera segons
 .
.
Aquesta relació és vàlida per a qualsevol
observador situat en un sistema inercial  ,
és a dir quan el mateix observador no està accelerat. El que passa
és que, quan les forces actuen sobre nosaltres mateixos, ens venen moltes
ganes de fer d'observadors. Però en aquest cas no serem un observador
inercial!
,
és a dir quan el mateix observador no està accelerat. El que passa
és que, quan les forces actuen sobre nosaltres mateixos, ens venen moltes
ganes de fer d'observadors. Però en aquest cas no serem un observador
inercial!
 La
llei de moviment de Newton per a un sistema no inercial
La
llei de moviment de Newton per a un sistema no inercial  ,
que es traslladi amb una acceleració (coneguda en funció del temps)
,
que es traslladi amb una acceleració (coneguda en funció del temps)
 respecte d'un sistema
inercial, resulta ser
respecte d'un sistema
inercial, resulta ser

on  és
la força d'inèrcia i
és
la força d'inèrcia i  la força exterior. Si a més considerem observadors no inercial
sotmesos a rotacions la llei de Newton s'embolica una mica més.
la força exterior. Si a més considerem observadors no inercial
sotmesos a rotacions la llei de Newton s'embolica una mica més.
Sobre un cos actua una força  causant
una acceleració
causant
una acceleració  , respecte d'un observador inercial. Si ens agafem a aquest cos i volem seguir
fent d'observador, serem no inercials
, respecte d'un observador inercial. Si ens agafem a aquest cos i volem seguir
fent d'observador, serem no inercials amb
amb  . Lògicament
no observarem cap acceleració en el cos malgrat estar afectat per una
força
. Lògicament
no observarem cap acceleració en el cos malgrat estar afectat per una
força  . També
li actua la força d'inercia
. També
li actua la força d'inercia ( vegeu la figura 2)!
( vegeu la figura 2)!
De tota manera, la tampoc no ens soluciona res del nostre cas, com veurem d'aquí una mica.
El problema no és aquest. Som lliures de fer física
des d'un observador inercial o des d'un de no inercial, sempre que escrivim
bé les equacions. Òbviament sempre és més
senzill fer-ho utilitzant un observador inercial i és aquest el que convé
que sigui sempre utilitzat per l'estudiantat. En aquest sentit no és
aconsellable que un estudiant s'observi ( físicament) a ell
mateix mentre viatja per una muntanya russa! Malgrat tot, voldrà trobar
una explicació a les sensacions rebudes... Podem donar aquesta explicació
més fàcilment des d'un sistema inercial.
tampoc no ens soluciona res del nostre cas, com veurem d'aquí una mica.
El problema no és aquest. Som lliures de fer física
des d'un observador inercial o des d'un de no inercial, sempre que escrivim
bé les equacions. Òbviament sempre és més
senzill fer-ho utilitzant un observador inercial i és aquest el que convé
que sigui sempre utilitzat per l'estudiantat. En aquest sentit no és
aconsellable que un estudiant s'observi ( físicament) a ell
mateix mentre viatja per una muntanya russa! Malgrat tot, voldrà trobar
una explicació a les sensacions rebudes... Podem donar aquesta explicació
més fàcilment des d'un sistema inercial.
La relativitat del moviment
La trajectòria dels objectes és relativa a l'observador.
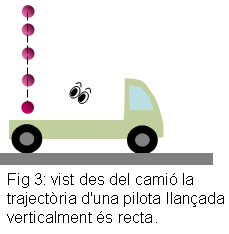
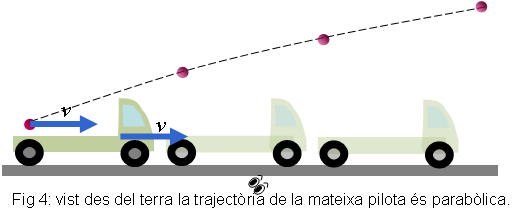
Aquí en tenim un parell d'exemples. En el primer cas ( figures 3 i 4),
un camió viatja a velocitat constant. Es llença una pilota des
del camió. Tant l'observador del camió com el del terra són
inercials, però observen trajectòries notablement diferents.
En el segon cas ( figura 5) un cotxe, després d'anar
per una recta, pren un revolt a velocitat de mòdul constant. La casset
que hi ha a sobre del tauler llisca respecte d'aquest. Segons l'observador del
cotxe (no inercial), la casset fa una trajectòria més o menys
recta i accelerada cap a la seva dreta. Una gavina vola en la direcció
de la recta, s'atura un moment sobre la corba (observador inercial) i observa
des de dalt (el cotxe és descapotable!) que la casset fa una trajectòria
recta i amb velocitat uniforme.
 |
| Fig 5: Un cotxe que pren un
revolt. A sobre el tauler porta una casset. |
El que és notable és que, en el primer cas, tan
l'observador del camió com el de terra aplicaran la mateixa llei de moviment
de Newton,  . Els dos
observadors són inercials. En canvi, en el segon cas, l'observador del
cotxe hauria d'aplicar una llei de moviment que tingués en compte que
no es tracta d'un observador inercial. Aquest observador no només es
trasllada sinó, que també gira. La seva llei de moviment (per
a descriure el moviment horitzontal) serà francament enrevessada, encara
que les forces externes (no inercials) siguin nul·les! Res a veure amb
la senzillesa de la llei de moviment d'un observador inercial qualsevol, sobretot
tenint en compte que les forces externes son nul·les:
. Els dos
observadors són inercials. En canvi, en el segon cas, l'observador del
cotxe hauria d'aplicar una llei de moviment que tingués en compte que
no es tracta d'un observador inercial. Aquest observador no només es
trasllada sinó, que també gira. La seva llei de moviment (per
a descriure el moviment horitzontal) serà francament enrevessada, encara
que les forces externes (no inercials) siguin nul·les! Res a veure amb
la senzillesa de la llei de moviment d'un observador inercial qualsevol, sobretot
tenint en compte que les forces externes son nul·les:  .
.
No és l'argument existencialista el que ens porta a
fer servir sistemes inercials. L'argument és de senzillesa. A la física
li costa molt discutir sobre temes absoluts. Li agrada mantenir-se en el debat
constant. És així com sorgeixen noves idees.Tinguem en compte
que hi ha un corrent de pensament (principi de Mach: http://en.wikipedia.org/wiki/Mach's_principle )
que associa les forces de l'inercia a la interacció deguda al moviment
relatiu respecte de la resta de l'univers. Vindria a dir que si no tinguessim
en compte la resta de l'univers, la casset de l'exemple anterior seguiria tranquil·lament
al lloc on la deixat el conductor malgrat estigui en ple revolt! Què
diria la gavina en aquest cas? Bé... sortosament tenim la resta de l'univers!
)
que associa les forces de l'inercia a la interacció deguda al moviment
relatiu respecte de la resta de l'univers. Vindria a dir que si no tinguessim
en compte la resta de l'univers, la casset de l'exemple anterior seguiria tranquil·lament
al lloc on la deixat el conductor malgrat estigui en ple revolt! Què
diria la gavina en aquest cas? Bé... sortosament tenim la resta de l'univers!
 Un
model de cos
Un
model de cos
Per poder continuar, construirem un model de cos (del nostre
cos) que tingui prous elements com per analitzar el pessigolleig, tot mantenint
un grau alt de simplicitat. En la figura 6 podem veure aquest model. Dues partícules
estan unides per una molla. Cada partícula té una massa diferent,
per si de cas. Una molla sense massa uneix aquestes dues partícules.
Podem pensar que la molla modelitza el nostre estómac que l'uneix a la
resta del cos.
La força que fa la molla sobre les partícules
és (els signes estan referits a la figura 6)

essent  la seva longitud natural i
la seva longitud natural i  la constant elàstica. Per una molla amb massa aquesta llei val tan si
la molla està en repòs o si està en moviment uniforme.
També val si la molla es mou acceleradament i no te massa ! Això
últim ens interessa per tal de simplificar el problema.
la constant elàstica. Per una molla amb massa aquesta llei val tan si
la molla està en repòs o si està en moviment uniforme.
També val si la molla es mou acceleradament i no te massa ! Això
últim ens interessa per tal de simplificar el problema.
Aquest model de cos ens permetrà identificar les sensacions
internes que sofrim amb les forces elàstiques ( internes!) del nostre
cos. Essencialment, en el nostre model, hem d'analitzar en cada cas la força
de la molla, o si ho preferim, els canvis de llargada que sofreix. Les forces
que molts cops atribuïm a l'inèrcia són les forces elàstiques
que aguanten unes parts del cos amb les altres. Vegem alguns casos típics.
 La
situació "normal"
La
situació "normal"
Per començar, simularem la situació en que ens
trobem normalment quan toquem de peus a Terra (figura 7). És remarcable
el fet que, en aquesta situació que anomenem normal, no només
estem sotmesos a la força pes, sinó que també estem sotmesos
a la normal!
Vegem que la longitud de la molla no és la natural.
Podem dir que "notem que pesem". Ara, com que hi estem tan acostumats,
no li donem més importància.
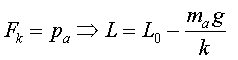
Caic lliurement
 Des
del terra del cas anterior ens llencem en caiguda lliure, és a dir, ens
desfem de la normal, tal com es veu en la figura 8. Pensem que inicialment la
longitud de la molla és la del cas anterior. Per evitar complicacions
innecessàries podem introduir un fregament viscós a la molla per
tal que no vagi oscil·lant tota l'estona. Així al cap de ben poc
d'iniciar la caiguda el cos sencer deixa de vibrar i es mou com un tot amb la
mateixa acceleració g.
És clar que ara
Des
del terra del cas anterior ens llencem en caiguda lliure, és a dir, ens
desfem de la normal, tal com es veu en la figura 8. Pensem que inicialment la
longitud de la molla és la del cas anterior. Per evitar complicacions
innecessàries podem introduir un fregament viscós a la molla per
tal que no vagi oscil·lant tota l'estona. Així al cap de ben poc
d'iniciar la caiguda el cos sencer deixa de vibrar i es mou com un tot amb la
mateixa acceleració g.
És clar que ara

és a dir, notem "que no pesem" però
que el nostre cos s'altera doncs a sofert un estirament respecte el cas anterior
de
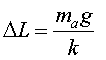
Si no haguèssim passat per la situació "normal"
no notaríem absolutament res: ens semblaria que no ens actua absolutament
cap força sobre nosaltres!
M'acceleren...
Essencialment tenim dues maneres d'accelerar un cos: empènyer-lo
per darrere o estirar-lo per davant.
 M'empenyen
M'empenyen
En aquest cas
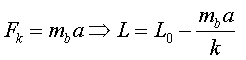
és a dir, ens encongim respecte de la longitud natural,
 .
.
 M'estiren
M'estiren
Ara
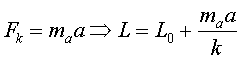
és a dir, ens estirem respecte de la longitud natural
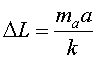
Em fan voltar uniformement en absència de gravetat...
Novament, hi ha dues maneres de concebre aquest moviment
 Amb
una corda
Amb
una corda
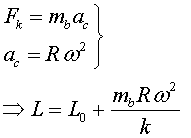
En aquest cas, i com podem esperar, el cos se’ns estira.
 Amb
un terra
Amb
un terra
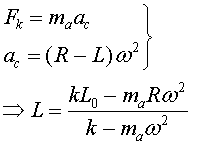
ara, és clar, ens encongim.
Autor
d'aquesta pągina: Xavier Jaén, professor
de físca de l'ETSEIB de la UPC.
Aquesta
obra estą subjecta a una
Llicčncia
de Creative Commons

 La
veritat és que és molt difícil convèncer els estudiants
que el pessigolleig que senten quan pugen a les muntanyes russes és degut
a unes forces que no existeixen. El problema sorgeix molt cops perquè
el debat queda tallat amb aquesta negació existencial tan severa. El
que podem fer és trobar explicacions a aquestes sensacions sense necessitat
de carregar les tintes amb qüestions existencials. En tot cas l'existència
o no d'aquestes forces dependrà de si les necessitem o no per explicar
el que ens envolta. Com passa en altre casos, la força no és un
concepte absolut.
La
veritat és que és molt difícil convèncer els estudiants
que el pessigolleig que senten quan pugen a les muntanyes russes és degut
a unes forces que no existeixen. El problema sorgeix molt cops perquè
el debat queda tallat amb aquesta negació existencial tan severa. El
que podem fer és trobar explicacions a aquestes sensacions sense necessitat
de carregar les tintes amb qüestions existencials. En tot cas l'existència
o no d'aquestes forces dependrà de si les necessitem o no per explicar
el que ens envolta. Com passa en altre casos, la força no és un
concepte absolut.  La
llei de moviment de Newton per a un sistema no inercial
La
llei de moviment de Newton per a un sistema no inercial 


 Un
model de cos
Un
model de cos La
situació "normal"
La
situació "normal"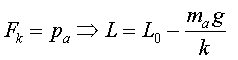
 Des
del terra del cas anterior ens llencem en caiguda lliure, és a dir, ens
desfem de la normal, tal com es veu en la figura 8. Pensem que inicialment la
longitud de la molla és la del cas anterior. Per evitar complicacions
innecessàries podem introduir un fregament viscós a la molla per
tal que no vagi oscil·lant tota l'estona. Així al cap de ben poc
d'iniciar la caiguda el cos sencer deixa de vibrar i es mou com un tot amb la
mateixa acceleració g.
És clar que ara
Des
del terra del cas anterior ens llencem en caiguda lliure, és a dir, ens
desfem de la normal, tal com es veu en la figura 8. Pensem que inicialment la
longitud de la molla és la del cas anterior. Per evitar complicacions
innecessàries podem introduir un fregament viscós a la molla per
tal que no vagi oscil·lant tota l'estona. Així al cap de ben poc
d'iniciar la caiguda el cos sencer deixa de vibrar i es mou com un tot amb la
mateixa acceleració g.
És clar que ara 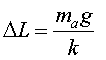
 M'empenyen
M'empenyen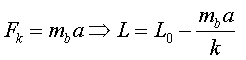
 .
.  M'estiren
M'estiren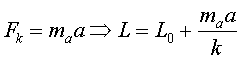
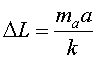
 Amb
una corda
Amb
una corda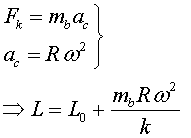
 Amb
un terra
Amb
un terra